Algorithms are all around us and used by academics and practitioners alike in many fields. The investment management industry too has been graced by the presence of mathematics and computers to better model and understand market dynamics. The emergence of machine learning brings up a question of how different these new algorithms truly are. Often machine learning is defined as a way to give computers the ability to learn without being explicitly programmed. This might sound far-fetched but developments are on their way. The ideology behind these new algorithms provides a way to reach that state. It’s a new way to approach a problem that ends up addressing the limitations of traditional statistical modeling.
Radically Different Assumptions
Traditional statistical methods were developed to implement the concept that understanding the underlying mechanism is sufficient to implement or predict future outcomes. Think of data as being generated by a black box given some other variables. Traditional methods assume that data follows a stochastic model (i.e., a tool for estimating probability distributions by allowing for random variations). So the response variables are a function of predictor variables, random noise, and parameters. The values of these parameters are estimated from the available data such that it makes as many correct predictions as possible.
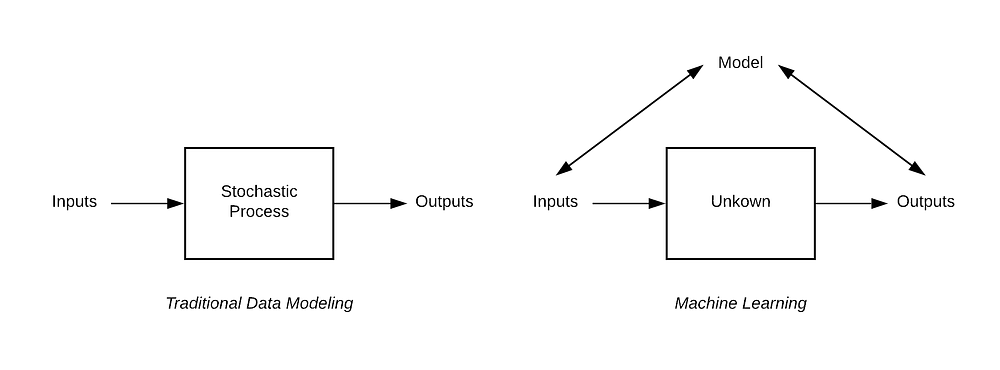
The new thinking that drives machine learning techniques is of the form that the black box is complex and unknown in comparison to previously assumed simple stochastic processes. This strikingly different assumption on the level of simplicity of the true unknown process has great significance and led to several debates in the scientific community. Traditional statistical modeling comes from a community that believes that the whole point of science is to open up black boxes, to better understand the underlying simple natural processes. Machine learning traces its origin from a rather practical community of young computer scientists, engineers, and statisticians. They focus on the output and favor precision and accuracy over interpretability.
A More Complex World
Prof. Leo Breiman, a distinguished statistician, notes that statisticians often see data modeling as a template for statistical analysis. That when faced with a problem, a statistician can devise a model that imitates a complex mechanism. Now, what’s left is to estimate parameters and draw conclusions. Prof. Breiman points out that when this model is to be evaluated, the conclusions are drawn about the model’s mechanism rather than the nature’s mechanism it was meant to emulate. He states, “The belief in the infallibility of data models was almost religious. It is a strange phenomenon — once a model is made, then it becomes truth and the conclusions from it are infallible.”
The Black-Scholes-Merton (BSM) model, a popular option pricing model still used today follows the traditional modeling approach. In BSM, a stock is chosen to follow Geometric Brownian motion. Assuming that the stock prices follow this natural stochastic process, researchers were able to derive a simple mechanism to price options. Interestingly, the model itself concludes that options are altogether redundant as they can be replicated by a portfolio of stocks and a bond. Yet, options trading is a multi-billion business. It’s because options carry risk which classical BSM ignores. The assumptions made of market completeness, continuous re-hedging, and zero transaction costs simplifies modeling but do not hold in practice. So, in reality, the true [unknown] mechanism followed by an option is different from what the entire BSM model is based on.
This method of addressing non-natural mechanisms goes back to when mathematics were incorporated into economics. George Soros writes, “Economics ended up with the theory of rational expectations, which maintains that there is a single optimum view of the future, that which corresponds to it, and eventually all the market participants will converge around that view. This postulate is absurd, but it is needed in order to allow economic theory to model itself on Newtonian physics.” The debate over the assumption of rational expectations in economic sciences has even brought up a sub-field of behavioral economics to work with practicality. It’s rather difficult to incorporate behavioral patterns in existing stochastic processes. However, machine learning that bases its solution directly from the observed data and not pinning it down to a natural stochastic process, could help economic sciences escape Newtonian physics that more often than not fails to understand market dynamics.
Prof. Igor Halperin at New York University uses reinforcement learning for discrete-time option pricing. Pricing is done by learning to dynamically optimize risk-adjusted returns for an option replicating portfolio. This method, the researcher states, can go model-free and learn to price and hedge an option directly from the data. Prof. Halperin finds that if the world is according to BSM, the model converges to the BSM price. Traditional methods do simplify black-boxes but are based on assumptions that generally do not hold true — at least in economic sciences. Machine learning, on the other hand, does not impose assumptions that restrict the ability of statisticians to deal with a wide range of problems.
Model Validation
Another major difference between the two methods lies in the way models are validated. In the traditional data modeling culture, a model is evaluated on a yes-no criterion using goodness-of-fit tests and residual analysis. It supposes that if a model passes a fitness test on the data it has been tested on, it will do a good prediction job. Machine learning, on the other hand, validates a model based on its predictive accuracy. It divides the data into two unequal parts. One on which the data is trained on and the other to check how well the trained model performs on prediction. Higher accuracy means a better model.
The validation approach in traditional statistics faces the problem of multiplicity. Rashomon is a Japanese movie in which four people, with different angles of observation, witness a crime. When they all testify in court, all report the same facts but different stories. Similarly, when the same dataset is given to different statisticians, they will come up with different mechanisms to represent the data and therefore different conclusions. Standard goodness-of-fit would not be able to help us prefer one over the other. Data will often point with almost equal emphasis on several possible models. Mountain and Hsiao (1989) write, “It is difficult to formulate a comprehensive model capable of encompassing all rival models. Furthermore, with the use of finite samples, there are dubious implications with regard to the validity and power of various encompassing tests that rely on asymptotic theory.”
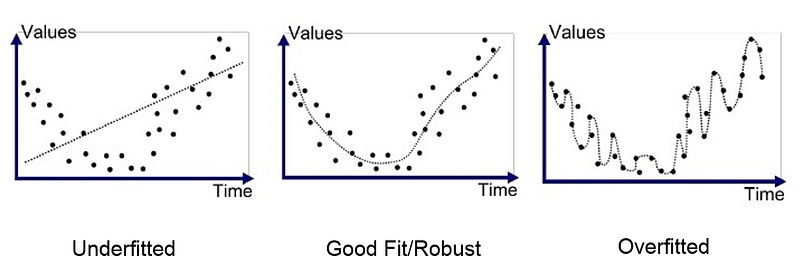
Machine learning practitioners take predictive accuracy very seriously. A model might seem good at first sight because it fits the data very well but it actually just overfits it. Overfitting could easily be understood by the image below. For this reason, test sets are used to remove bias while evaluating a model and make sure the trained model is not, in fact, overfitted. All machine learning methods contain some form of parameter tuning. The issue here is that with experience, analysts learn how to set the tuning parameters in order to get the best test results. Leaking information from test data to training data is very easy. Both in industry and academia, there is always a little tinkering. This may be deliberate or a result of not following the procedure diligently. Even a glimpse at test data could create a bias that analysts could use to their advantage for modeling or parameter tuning. This kind of tinkering easily invalidates the model selection.
Machine learning methods have the advantage of having a mechanism to judge the predicting power of a model but it comes with a strict need for ethics. While handling data, researchers need to follow a strict code of ethics. This means no peeking. Unfortunately, there’s no way to tell if the information was knowingly or unknowingly leaked unless there’s a separate dataset that the researcher didn’t have access to. Even then, high performance on the test sample does not guarantee high performance on future samples, but there are practices that can be followed to protect against change. If there is a lack of high ethical standards while using these models, this field of study would not create the required developments as practitioners wouldn’t get the benefits they promise.
Conclusion
The biggest criticism that machine learning and related methods face is on their interpretability. There seems to be a trade-off between accuracy and understanding. Prof. Breiman, however, argues, “framing the question as the choice between accuracy and interpretability is an incorrect interpretation of what the goal of statistical analysis is. The point of a model is to get useful information about the relation between the response and predictor variables. Interpretability is a way of getting information. But a model does not have to be simple to provide reliable information about the relationship between predictor and response variables.” He mentions, “the goal is not interpretability, but accurate information.” When argued against that the goal of science is to open black boxes, Prof. Breiman refutes it by stating that the evolution of science is from simple to complex.
The enthusiastic community of computer scientists and engineers have brought up another culture in statistical modeling. Both the approaches differ right in the philosophy behind approaching a problem. This has led them to possess different qualities. One stands out at simplicity and ease of understanding but at the expense of over-simplification. Another stems to produce accuracy and practical implementation but at the expense of interpretability. Machine learning promises both the industry and academia with practical mathematics in decision sciences. For economics, it provides a solution to escape the rational expectation assumption that it perforce accepted to be able to get scientific. In investing, it’s an opportunity to get increasingly systematic and increase an algorithm’s ability to handle risk. However, without addressing the ethical standards required while learning from the data, this promise would be left unfulfilled and be instead filled with an overdose of skepticism.
Sources
Breiman, L. (2001). Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Statistical Science, 16(3), 199–231. doi: 10.1214/ss/1009213726
Halperin, I. (2017). QLBS: Q-Learner in the Black-Scholes (-Merton) Worlds. SSRN Electronic Journal. doi: 10.2139/ssrn.3087076
Soros, G. (2010). The Soros lectures. New York: BBS/PublicAffairs
Mountain, D., & Hsiao, C. (1989). A Combined Structural and Flexible Functional Approach for Modeling Energy Substitution. Journal Of The American Statistical Association, 84(405), 76. doi: 10.2307/2289848
The views expressed above are not necessarily the views of Thalēs Trading Solutions or any of its affiliates (collectively, “Thalēs”). The information presented above is only for informational and educational purposes and is not an offer to sell or the solicitation of an offer to buy any securities or other instruments. Additionally, the above information is not intended to provide, and should not be relied upon for investment, accounting, legal or tax advice. Thalēs makes no representations, express or implied, regarding the accuracy or completeness of this information, and the reader accepts all risks in relying on the above information for any purpose whatsoever.






